Bấm Máy Tính Nhị Thức Newton: Hướng Dẫn Chi Tiết A-Z

Nền Tảng Lý Thuyết Nhị Thức Newton Cần Nắm Vững

Nhị thức Newton, hay công thức khai triển Newton, cung cấp một phương pháp hệ thống để khai triển lũy thừa bậc cao của một tổng hai số hạng (a + b)^n. Đây là công cụ toán học mạnh mẽ, được ứng dụng rộng rãi trong nhiều lĩnh vực từ đại số, giải tích đến xác suất thống kê. Để có thể áp dụng hiệu quả kỹ thuật bấm máy tính nhị thức Newton, việc hiểu rõ bản chất công thức là vô cùng cần thiết.

Với n là số nguyên dương và a, b là các số thực (hoặc biểu thức), ta có công thức khai triển tổng quát như sau:

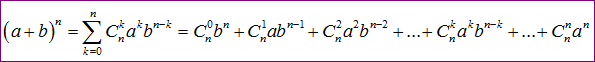công thức nền tảng cách bấm máy tính nhị thức newton

Công thức trên cho thấy khai triển của (a+b)^n là tổng của n+1 số hạng. Mỗi số hạng có dạng $C{n}^{k} a^{n-k} b^k$, trong đó $C{n}^{k}$ là tổ hợp chập k của n phần tử (hay hệ số nhị thức), $a^{n-k}$ là lũy thừa của số hạng đầu tiên và $b^k$ là lũy thừa của số hạng thứ hai. Vai trò của a và b trong công thức là tương đương, cho phép chúng ta hoán đổi vị trí của chúng để có một công thức khai triển tương đương, đôi khi giúp việc tính toán trở nên thuận tiện hơn.

công thức nền tảng cách bấm máy tính nhị thức newton hoán đổi ab

Xem Thêm Bài Viết:

• Địa Chỉ IP Là Gì? Hướng Dẫn Cực Kỳ Đơn Giản Cho Người Mới Bắt Đầu
• Lịch Sử Máy Tính Đầu Tiên ENIAC: Cột Mốc Vĩ Đại Mở Ra Kỷ Nguyên Số
• Cách Chỉnh Máy In Cho Đậm Mực Chuẩn Nhất
• Máy in không in được: Nguyên nhân và cách sửa lỗi triệt để
• Đổ mực máy in tại Thanh Xuân: Nhanh, Rẻ

Việc áp dụng công thức nhị thức Newton không chỉ dừng lại ở các biểu thức phức tạp mà còn giúp ta khai triển một số hằng đẳng thức quen thuộc một cách dễ dàng và chính xác. Đây là bước đệm quan trọng để hiểu sâu hơn về cấu trúc của các biểu thức đa thức và là nền tảng khi chúng ta bắt đầu thực hiện các thao tác bấm máy tính nhị thức Newton cho những bài toán cụ thể.

khai triển hằng đẳng thức – cách bấm máy tính nhị thức newton

Hướng Dẫn Chi Tiết Cách Bấm Máy Tính Nhị Thức Newton

Việc sử dụng máy tính cầm tay (CASIO hoặc các dòng tương tự) là một kỹ năng thiết yếu giúp học sinh rút ngắn đáng kể thời gian giải toán, đặc biệt với các bài tập yêu cầu tìm hệ số của một số hạng cụ thể trong khai triển nhị thức Newton. Phương pháp bấm máy tính nhị thức Newton thông qua chức năng TABLE (MODE 7) là một trong những cách hiệu quả nhất.

Ví Dụ 1: Tìm Số Hạng Chứa $x^{40}$ trong Khai Triển $(x^3-frac{2}{x^2})^{15}$

Để tìm số hạng chứa $x^{40}$ trong khai triển nhị thức Newton của $(x^3-frac{2}{x^2})^{15}$ với $x ne 0$, chúng ta sẽ thực hiện các bước sau trên máy tính CASIO, tận dụng chức năng TABLE.

Thông thường, khi giải tự luận, bạn sẽ áp dụng công thức số hạng tổng quát thứ $k+1$ là $T{k+1} = C{n}^{k} a^{n-k} b^k$. Trong trường hợp này, $n=15$, $a=x^3$, $b=-frac{2}{x^2} = -2x^{-2}$. Khi đó, số hạng tổng quát sẽ là:

$T{k+1} = C{15}^{k} (x^3)^{15-k} (-2x^{-2})^k = C{15}^{k} (-2)^k x^{3(15-k)} x^{-2k} = C{15}^{k} (-2)^k x^{45-3k-2k} = C_{15}^{k} (-2)^k x^{45-5k}$

Để tìm số hạng chứa $x^{40}$, ta cần $45-5k = 40$, suy ra $5k = 5$, vậy $k=1$. Từ đây, có thể suy ra cách giải bằng CASIO sử dụng TABLE như sau:

Bước 1: Khởi Động Chức Năng TABLE
Trên máy tính CASIO (ví dụ: fx-570VN PLUS, fx-580VN X), bạn vào MODE và chọn chức năng TABLE (thường là số 7). Đảm bảo rằng cả f(x) và g(x) đều được bật, điều này có thể cần cài đặt ban đầu hoặc bật thủ công tùy dòng máy.

Bước 2: Nhập Hàm Hệ Số vào f(x)
Phần hệ số của số hạng tổng quát là $C{15}^{k} (-2)^k$. Trong máy tính, chúng ta sẽ thay $k$ bằng biến X.
Nhập vào f(x): $C{15}^{X} (-2)^X$. (Cụ thể trên máy là 15 SHIFT chia X nhân (-2)^X).

Bước 3: Nhập Hàm Mũ của x vào g(x)
Phần mũ của x là $x^{45-5k}$. Chúng ta muốn tìm k sao cho mũ này bằng 40. Tuy nhiên, để tiện lợi khi dùng TABLE, chúng ta sẽ đưa biểu thức mũ $45-5X$ vào g(x) và tìm giá trị X nào làm cho g(x) = 40.
Nhập vào g(x): $45-5X$.
Thiết lập khoảng giá trị cho X (biến k):

• START (Giá trị bắt đầu của k): 0 (vì k bắt đầu từ 0)
• END (Giá trị kết thúc của k): 15 (vì k tối đa bằng n, ở đây n=15)
• STEP (Bước nhảy): 1 (vì k là số nguyên)

cách bấm máy tính nhị thức newton

Bước 4: Kiểm Tra Kết Quả
Sau khi thiết lập, máy tính sẽ hiển thị một bảng giá trị. Bạn đẩy con trỏ xuống cột g(x) để tìm giá trị bằng 40. Khi g(x) = 40, hãy nhìn sang cột X tương ứng để tìm giá trị của k.

Khi g(x) = 40, ta thấy X = 1. Giá trị này chính là k cần tìm. Bây giờ, nhìn sang cột f(x) tại dòng có X = 1, ta sẽ thấy hệ số tương ứng. Giá trị hiển thị là -30.

Như vậy, hệ số của số hạng chứa $x^{40}$ là -30. Việc sử dụng kỹ thuật bấm máy tính nhị thức Newton này giúp chúng ta nhanh chóng xác định k và hệ số mà không cần thực hiện nhiều phép tính tay phức tạp.

Ví Dụ 2: Tìm Hệ Số của $x^4$ Với n Ẩn

Tìm hệ số của $x^4$ trong khai triển nhị thức Newton $(x^3-frac{2}{x^2})^n$ (với $x>0$), biết n là số tự nhiên thỏa mãn phương trình: $A{n}^{2}+C{n}^{n-1}+C_{n}^{n-2}=92$.

Đây là một bài toán hai bước. Bước đầu tiên là tìm giá trị của n bằng cách giải phương trình tổ hợp, và bước thứ hai là tìm hệ số của $x^4$ với n đã biết.

Bước 1: Dùng TABLE để tìm n
Thay vì giải phương trình tổ hợp bằng tay, chúng ta có thể sử dụng chức năng TABLE của máy tính để tìm n.
Nhập hàm $f(X) = A{X}^{2}+C{X}^{X-1}+C_{X}^{X-2}$ vào máy tính.
Thiết lập khoảng chạy:

• START: 2 (vì $A_n^2$ yêu cầu $n ge 2$)
• END: Khoảng 15-20 (thử một khoảng đủ rộng, ví dụ 10)
• STEP: 1

cách bấm máy tính nhị thức newton

Sau khi chạy bảng, chúng ta sẽ tìm giá trị X nào làm cho $f(X) = 92$.

cách bấm máy tính nhị thức newton

Quan sát bảng, ta thấy khi X = 8, f(X) = 92. Vậy, n = 8.

Bước 2: Tìm hệ số của $x^4$ với n = 8
Bây giờ bài toán quay về dạng Ví dụ 1, nhưng với $n=8$. Khai triển là $(x^3-frac{2}{x^2})^8$.
Số hạng tổng quát: $T{k+1} = C{8}^{k} (x^3)^{8-k} (-2x^{-2})^k = C{8}^{k} (-2)^k x^{3(8-k)-2k} = C{8}^{k} (-2)^k x^{24-5k}$.
Để tìm số hạng chứa $x^4$, ta cần $24-5k = 4$, suy ra $5k = 20$, vậy $k=4$.

Tiến hành bấm máy tính nhị thức Newton tương tự Ví dụ 1:

• f(x): $C_{8}^{X} (-2)^X$
• g(x): $24-5X$
• START=0, END=8, STEP=1

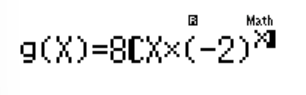cách bấm máy tính nhị thức newton

Tìm X = 4 trong bảng của g(x) = 4, sau đó nhìn sang cột f(x) để lấy hệ số.

cách bấm máy tính nhị thức newton

cách bấm máy tính nhị thức newton

Khi X = 4, g(x) = 4, và f(x) = 1120. Vậy, hệ số của $x^4$ là 1120.

Ví Dụ 3: Tìm Hệ Số của $x^{10}$ Với n Ẩn Khác

Tìm hệ số của $x^{10}$ trong khai triển nhị thức Newton của $(2+x)^n$, biết:
$C{n}^{1}+2C{n}^{2}+3C{n}^{3}+…+nC{n}^{n}=256n$

Phương trình đã cho là một đẳng thức đặc biệt. Để giải, chúng ta cần nhớ một số tính chất của tổ hợp. Ta biết rằng $kCn^k = nC{n-1}^{k-1}$. Áp dụng tính chất này vào vế trái của đẳng thức, ta có:
$C{n}^{1}+2C{n}^{2}+3C{n}^{3}+…+nC{n}^{n} = sum_{k=1}^{n} kCn^k = sum{k=1}^{n} nC{n-1}^{k-1}$
Đặt $j = k-1$, khi $k=1 Rightarrow j=0$, khi $k=n Rightarrow j=n-1$.
Vậy, $sum{j=0}^{n-1} nC{n-1}^{j} = n sum{j=0}^{n-1} C_{n-1}^{j} = n cdot 2^{n-1}$.
Từ đẳng thức ban đầu: $n cdot 2^{n-1} = 256n$.
Vì n là số tự nhiên và thường $n ne 0$ trong các bài toán nhị thức, ta có thể chia cả hai vế cho n:
$2^{n-1} = 256$
$2^{n-1} = 2^8$
$n-1 = 8 Rightarrow n = 9$.

Bây giờ ta đã có $n=9$. Khai triển là $(2+x)^9$.
Số hạng tổng quát: $T{k+1} = C{9}^{k} 2^{9-k} x^k$.
Để tìm số hạng chứa $x^{10}$, ta cần $k=10$. Tuy nhiên, ở đây $k$ chỉ chạy từ 0 đến $n=9$. Do đó, không có số hạng nào chứa $x^{10}$ trong khai triển này. Hệ số của $x^{10}$ là 0.

Đây là một ví dụ minh họa cho việc hiểu lý thuyết là quan trọng như thế nào, ngay cả khi chúng ta thành thạo việc bấm máy tính nhị thức Newton. Máy tính chỉ là công cụ hỗ trợ, kiến thức nền tảng vẫn là chìa khóa.

Ví dụ 3 cách bấm máy tính nhị thức newton

Trong trường hợp bạn muốn dùng CASIO để kiểm tra giá trị n, bạn có thể nhập $f(X) = X cdot 2^{X-1} – 256X$ vào chức năng TABLE và tìm giá trị X nào làm cho $f(X)=0$.
Thiết lập:

• START: 1
• END: 10
• STEP: 1

Giải ví dụ 3 bằng cách bấm máy tính nhị thức newton

Khi kiểm tra bảng, bạn sẽ thấy tại X = 9, giá trị f(X) = 0. Vậy n=9 là chính xác.

Luyện Tập Giải Bài Tập Nhị Thức Newton Bằng CASIO

Để thành thạo kỹ năng bấm máy tính nhị thức Newton, việc luyện tập qua các dạng bài tập khác nhau là điều cần thiết. Dưới đây là một số bài tập minh họa kèm hướng dẫn giải nhanh bằng CASIO.

Bài 1: Tìm Hệ Số $x^5$ trong Khai Triển $f(x)=(x^3-frac{2}{x})^n$

Cho n là số tự nhiên thỏa mãn $2C{n}^{1}-C{n}^{2}+n=0$. Tìm hệ số $x^5$ sau khi khai triển biểu thức $f(x)=(x^3-frac{2}{x})^n$.

Hướng dẫn giải:
Bước 1: Tìm n
Sử dụng chức năng TABLE để giải phương trình $2C{n}^{1}-C{n}^{2}+n=0$.
Nhập $f(X) = 2C{X}^{1}-C{X}^{2}+X$ vào máy tính.
Thiết lập khoảng chạy: START=2, END=10, STEP=1.
Kiểm tra bảng giá trị, ta thấy khi X = 7, $f(X) = 0$. Vậy n = 7.

Bước 2: Tìm hệ số $x^5$
Với n=7, biểu thức khai triển là $f(x)=(x^3-2x^{-1})^7$.
Số hạng tổng quát: $T{k+1} = C{7}^{k} (x^3)^{7-k} (-2x^{-1})^k = C{7}^{k} (-2)^k x^{3(7-k)-k} = C{7}^{k} (-2)^k x^{21-4k}$.
Để tìm hệ số $x^5$, ta cần $21-4k = 5$, suy ra $4k = 16$, vậy $k=4$.

Sử dụng CASIO để tính $C{7}^{4} (-2)^4$:
Nhập $C{7}^{X} (-2)^X$ vào f(x) và $21-4X$ vào g(x) với START=0, END=7, STEP=1.
Tìm X = 4 trong bảng ứng với g(x) = 5.
Giá trị f(x) tại X = 4 là 560.

Bài 1 cách bấm máy tính nhị thức newton

Kết luận: Hệ số của $x^5$ là 560.

Bài 2: Tìm Hệ Số $x^7$ với n Ẩn và Biểu Thức Khác

Cho n là số nguyên dương thỏa mãn $4C{n-1}^{3}+2C{n}^{2}=A_{n}^{3}$. Tìm hệ số $x^7$ sau khi khai triển biểu thức $f(x)=(x^2-frac{2}{x})^n$.

Hướng dẫn giải:
Bước 1: Tìm n
Tương tự như các ví dụ trên, sử dụng chức năng TABLE để tìm n.
Nhập $f(X) = 4C{X-1}^{3}+2C{X}^{2}-A{X}^{3}$ vào máy tính. Lưu ý rằng $C{n-1}^3$ yêu cầu $n-1 ge 3 Rightarrow n ge 4$, và $A_n^3$ yêu cầu $n ge 3$. Vậy, START=4.
Thiết lập khoảng chạy: START=4, END=15, STEP=1.
Khi kiểm tra bảng, ta thấy phương trình có nghiệm n=11.

Bước 2: Tìm hệ số $x^7$
Với n=11, biểu thức khai triển là $f(x)=(x^2-2x^{-1})^{11}$.
Số hạng tổng quát: $T{k+1} = C{11}^{k} (x^2)^{11-k} (-2x^{-1})^k = C{11}^{k} (-2)^k x^{2(11-k)-k} = C{11}^{k} (-2)^k x^{22-3k}$.
Để tìm hệ số $x^7$, ta cần $22-3k = 7$, suy ra $3k = 15$, vậy $k=5$.

Sử dụng CASIO để tính $C{11}^{5} (-2)^5$:
Nhập $C{11}^{X} (-2)^X$ vào f(x) và $22-3X$ vào g(x) với START=0, END=11, STEP=1.
Tìm X = 5 trong bảng ứng với g(x) = 7.
Giá trị f(x) tại X = 5 là -14784.

Bài 2 cách bấm máy tính nhị thức newton

Vậy, hệ số của $x^7$ là -14784.

Bài 3: Tìm Hệ Số $x^4$ trong Khai Triển Đa Thức $f(x)=(1+2x+3x^2)^{10}$

Đây là một dạng bài khai triển đa thức, không phải nhị thức Newton trực tiếp. Tuy nhiên, chúng ta vẫn có thể áp dụng nguyên lý tương tự và kết hợp cách bấm máy tính nhị thức Newton cho từng phần nếu cần.

Hướng dẫn giải:
Đặt $(1+2x+3x^2)^{10} = ((1+2x) + 3x^2)^{10}$.
Theo công thức nhị thức Newton, số hạng tổng quát của khai triển này là $C{10}^{k} (1+2x)^{10-k} (3x^2)^k$.
Để có $x^4$, chúng ta cần tổng lũy thừa của x trong mỗi số hạng bằng 4.
$C{10}^{k} (1+2x)^{10-k} (3x^2)^k = C{10}^{k} 3^k x^{2k} (1+2x)^{10-k}$.
Giờ chúng ta cần tìm số hạng chứa $x^{4-2k}$ trong khai triển $(1+2x)^{10-k}$.
Số hạng tổng quát của $(1+2x)^{10-k}$ là $C{10-k}^{j} (1)^{10-k-j} (2x)^j = C{10-k}^{j} 2^j x^j$.
Vậy, ta cần $j = 4-2k$.
Kết hợp lại, số hạng chứa $x^4$ sẽ có dạng:
$C{10}^{k} 3^k C_{10-k}^{j} 2^j x^{2k+j}$ với $2k+j=4$.
Ta cần tìm các cặp (k, j) thỏa mãn $2k+j=4$ và các điều kiện về chỉ số:

• $0 le k le 10$
• $0 le j le 10-k$
• $k, j$ là số nguyên không âm.

Các trường hợp có thể:

• Nếu $k=0 Rightarrow j=4$. Hệ số: $C{10}^{0} 3^0 C{10}^{4} 2^4 = 1 cdot 1 cdot 210 cdot 16 = 3360$.
• Nếu $k=1 Rightarrow j=2$. Hệ số: $C{10}^{1} 3^1 C{9}^{2} 2^2 = 10 cdot 3 cdot 36 cdot 4 = 4320$.
• Nếu $k=2 Rightarrow j=0$. Hệ số: $C{10}^{2} 3^2 C{8}^{0} 2^0 = 45 cdot 9 cdot 1 cdot 1 = 405$.
• Nếu $k ge 3$, thì $j < 0$, không hợp lệ.

Tổng các hệ số: $3360 + 4320 + 405 = 8085$.

Bài 3 cách bấm máy tính nhị thức newton

Kết luận: Hệ số của $x^4$ bằng 8085.

Bài 4: Tìm Số Hạng Chứa $x^{14}$ trong Khai Triển $f(x)=(1+x+3x^2)^n$

Cho n là số nguyên dương thỏa mãn: $C{n}^{1}+C{n}^{2}+C{n}^{3}+…+C{n}^{n}=255$. Tìm số hạng chứa $x^{14}$ trong khai triển của biểu thức: $f(x)=(1+x+3x^2)^n$.

Hướng dẫn giải:
Bước 1: Tìm n
Ta có công thức khai triển nhị thức Newton: $(1+1)^n = C_n^0 + C_n^1 + C_n^2 + … + Cn^n = 2^n$.
Từ đẳng thức đã cho: $C{n}^{1}+C{n}^{2}+C{n}^{3}+…+C_{n}^{n}=255$.
Đây chính là $2^n – C_n^0 = 255$. Vì $C_n^0=1$, nên $2^n-1=255 Rightarrow 2^n=256 Rightarrow n=8$.

Bước 2: Tìm số hạng chứa $x^{14}$
Với n=8, biểu thức khai triển là $f(x)=(1+x+3x^2)^8$.
Đặt $A = 1+x$ và $B = 3x^2$. Ta có $(A+B)^8$.
Số hạng tổng quát của khai triển này là $C{8}^{k} (1+x)^{8-k} (3x^2)^k = C{8}^{k} 3^k x^{2k} (1+x)^{8-k}$.
Để có $x^{14}$, chúng ta cần tìm số hạng chứa $x^{14-2k}$ trong khai triển $(1+x)^{8-k}$.
Số hạng tổng quát của $(1+x)^{8-k}$ là $C{8-k}^{j} (1)^{8-k-j} x^j = C{8-k}^{j} x^j$.
Vậy, ta cần $j = 14-2k$.
Tổng số mũ của x là $2k+j = 2k + (14-2k) = 14$.
Ta cần tìm các cặp (k, j) thỏa mãn $j=14-2k$ và các điều kiện:

• $0 le k le 8$
• $0 le j le 8-k$
• $k, j$ là số nguyên không âm.

Các trường hợp có thể:

• Nếu $k=3 Rightarrow j=14-2(3)=8$. Điều kiện $0 le 8 le 8-3=5$ (SAI, vì $8 > 5$).
• Nếu $k=4 Rightarrow j=14-2(4)=6$. Điều kiện $0 le 6 le 8-4=4$ (SAI, vì $6 > 4$).
• Nếu $k=5 Rightarrow j=14-2(5)=4$. Điều kiện $0 le 4 le 8-5=3$ (SAI, vì $4 > 3$).
• Nếu $k=6 Rightarrow j=14-2(6)=2$. Điều kiện $0 le 2 le 8-6=2$ (ĐÚNG). Hệ số: $C{8}^{6} 3^6 C{2}^{2} = 28 cdot 729 cdot 1 = 20412$.
• Nếu $k=7 Rightarrow j=14-2(7)=0$. Điều kiện $0 le 0 le 8-7=1$ (ĐÚNG). Hệ số: $C{8}^{7} 3^7 C{1}^{0} = 8 cdot 2187 cdot 1 = 17496$.
• Nếu $k ge 8$, thì $j < 0$ hoặc $j$ không đủ điều kiện.

Tổng các hệ số: $20412 + 17496 = 37908$.

Kết luận: Hệ số của $x^{14}=37908$.

kết luận bài 4 cách bấm máy tính nhị thức newton

Bài 5: Tìm Số Hạng Chứa $x^6$ Với Đẳng Thức Phức Tạp

Tìm số hạng chứa $x^6$ trong khai triển nhị thức Newton của đẳng thức sau (sử dụng cách bấm máy tính nhị thức Newton):
$f(x) = (1+2x)^2 (x^2+x+1)^2$
Biểu thức gốc: $f(x)=(1+2x)^{10}(x^2+x+1)^2$. Có vẻ có sự nhầm lẫn giữa đề bài và cách giải trong bài gốc. Tôi sẽ bám sát cách giải đã cho để làm rõ. Nếu đề bài là $(1+2x)^{10}(x^2+x+1)^2$, thì phép biến đổi sau đó:
$x^2+x+1=frac{(2x+1)^2+3}{4}$. Do đó:
$f(x)=(1+2x)^{10} left(frac{(2x+1)^2+3}{4}right)^2$
$f(x)=frac{1}{16}(1+2x)^{10} ((1+2x)^2+3)^2$
$f(x)=frac{1}{16}(1+2x)^{10} ((1+2x)^4 + 6(1+2x)^2 + 9)$
$f(x)=frac{1}{16}(1+2x)^{14} + frac{6}{16}(1+2x)^{12} + frac{9}{16}(1+2x)^{10}$
$f(x)=frac{1}{16}(1+2x)^{14} + frac{3}{8}(1+2x)^{12} + frac{9}{16}(1+2x)^{10}$

Chúng ta cần tìm hệ số của $x^6$ trong mỗi phần của tổng này.
Số hạng tổng quát của $(1+2x)^n$ là $C_n^k (1)^k (2x)^k = C_n^k 2^k x^k$.
Để tìm hệ số của $x^6$, ta cần $k=6$.

• Phần 1: $frac{1}{16}(1+2x)^{14}$
  Hệ số $x^6$: $frac{1}{16} C_{14}^{6} 2^6 = frac{1}{16} cdot 3003 cdot 64 = 3003 cdot 4 = 12012$.
• Phần 2: $frac{3}{8}(1+2x)^{12}$
  Hệ số $x^6$: $frac{3}{8} C_{12}^{6} 2^6 = frac{3}{8} cdot 924 cdot 64 = 3 cdot 924 cdot 8 = 22176$.
• Phần 3: $frac{9}{16}(1+2x)^{10}$
  Hệ số $x^6$: $frac{9}{16} C_{10}^{6} 2^6 = frac{9}{16} cdot 210 cdot 64 = 9 cdot 210 cdot 4 = 7560$.

Tổng các hệ số: $12012 + 22176 + 7560 = 41748$.

Kết luận bài 5 cách bấm máy tính nhị thức newton

Kết luận: Hệ số của $x^6$ là 41748.

Trong quá trình giải các bài toán trên, việc hiểu rõ lý thuyết và áp dụng linh hoạt các chức năng của máy tính cầm tay là chìa khóa. Kỹ năng bấm máy tính nhị thức Newton không chỉ giúp bạn giải nhanh mà còn giúp kiểm tra lại kết quả của các bài toán tự luận, nâng cao độ chính xác trong học tập và thi cử. Các loại máy tính hỗ trợ tính toán tổ hợp và hàm số như Casio FX-570VN PLUS, Casio FX-580VN X đều là những công cụ đắc lực mà bạn có thể tìm hiểu thêm tại lavender-panther-755911.hostingersite.com.

Việc thành thạo các kỹ năng bấm máy tính nhị thức Newton sẽ giúp bạn tiết kiệm thời gian đáng kể và tăng cường độ chính xác khi đối mặt với các bài tập từ cơ bản đến nâng cao. Hy vọng rằng qua bài viết này, bạn đã có thể nắm vững cả lý thuyết lẫn cách ứng dụng máy tính cầm tay để giải quyết các vấn đề liên quan đến nhị thức Newton một cách hiệu quả nhất.